Tahukah kamu seperti apa rumus luas selimut tabung? Tabung atau silinder adalah salah satu bangun ruang yang memiliki selimut, yaitu sisi lengkung yang melingkupi permukaan tabung. Untuk mencari besar luasannya, maka dihitung dengan menggunakan rumus. Dengan rumus tersebut, kita bisa menghitung berapa luas selimut sebuah tabung, baik tabung yang berdimensi kecil, maupun besar.

Sebenarnya, jika kita memahami sifat-sifat tabung, maka kita bisa dengan mudah mencari atau menurunkan sendiri rumus luas selimut tabung. Sebagaimana yang diketahui, tabung adalah bangun ruang yang hanya memiliki 3 sisi. Dua sisi berfungsi sebagai alas dan tutup, satu lagi berfungsi sebagai selimut tabung.
Berdasarkan penelusuran kami, telah banyak blog atau website yang mengulas rumus luas selimut tabung. Tetapi, kekurangan dari blog-blog tersebut adalah mereka tidak memberikan penjelasan tentang bagaimana cara mencari atau menurun rumus tersebut. Padahal, hal ini termasuk penting, agar pembaca bisa mendapatkan pemahaman yang baik tentang selimut tabung.
Nah, olehnya itu pada kesempatan kali ini, kami tidak hanya memberikan rumus luas selimut tabung, tetapi kami juga akan menunjukkan kepada pembaca bagaimana rumus tersebut ditemukan. Semoga setelah membaca uraian ini, pengetahuan pembaca tentang selimut tabung semakin bertambah.
Baca Juga:
Yuk, berikut ini ulasannya...
Selimut Tabung
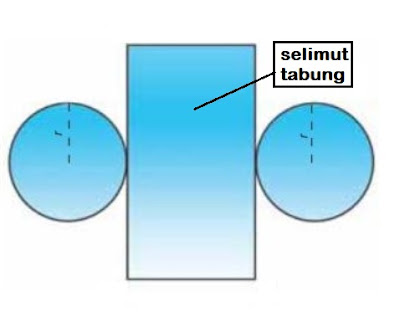
Cobalah ambil sebuah tabung, dan perhatikan semua sisinya. Sekarang, tunjukkan yang mana bagian selimutnya. Yah Benar, selimut dari sebuah tabung adalah bidang lengkung yang menutupi bagian samping tabung. Selimut tabung menjadi penghubung antara bagian atas tabung (tutup) dengan bagian bawahnya (tutup). Perhatikan gambar berikut ini:

Gambar di atas, memperlihatkan bagian-bagian dari sebuah tabung yang terdiri dari tutup, selimut, dan alas tabung. Bagian selimut inilah yang akan kita cari luasnya.
1. Luas Selimut Tabung
Setelah memperhatikan gambar tabung di atas, kira-kira bagaimana cara menentukan luas selimutnya? Strategi paling mudah adalah kita bongkar tabungnya, pisahkan bagian-bagiannya, dan mengambil selimutnya untuk diukur luasnya. Pemisahan bagian-bagian tabung ini dipelajari dalam materi jaring-jaring tabung.
Cara membuat jaring-jaring tabung adalah mengiris bagian rusuk tabung untuk membuka bagiannya. Berikut ini adalah gambar jaring-jaring tabung setelah dilakukan irisan:
Setelah membuka semua bagian tabung, kemudian merebahkannya sampai membentuk bidang datar, ternyata bagian selimut tabung dibentuk oleh satu persegi panjang. Sehingga, bisa kita katakan bahwa luas selimut tabung sama dengan luas persegi panjang tersebut, yang bisa dihitung dengan cara mengalikan antara panjang dan lebar persegi panjang.
Perhitungan di atas dimungkinkan saat kita bisa membuka seluruh bagian tabung. Tetapi, bagaimana cara menghitung luas selimut tabung tanpa harus membuka bagian-bagiannya? Karena itulah, kita perlu untuk menurunkan rumusnya.
2. Menurunkan Rumus Luas Selimut Tabung
Setelah mengetahui bahwa selimut tabung terbentuk dari satu buah persegi panjang, maka kita bisa mulai menurunkan rumusnya dengan mengikuti susunan rumus luas persegi panjang.
Luas Persegi Panjang = Panjang x Lebar
Agar terbentuk sebuah tabung, persegi panjang harus dilengkungkan sampai bertemu kedua ujungnya. Setelah dilengkungkan, persegi panjang tersebut telah berbentuk melingkar dengan jari-jari tertentu dari titik pusat. Saat seluruh pekerjaan ini diteruskan dengan menambahkan dua buah lingkaran untuk menutupi bagian atas dan bawahnya, maka akan terbentuk bangun ruang tabung.
Persegi panjang yang telah melengkung tersebut selanjutnya kita sebut selimut tabung, panjang persegi panjang kita sebut panjang selimut tabung, dan lebar persegi panjang kita sebut tinggi tabung. Dengan mengikuti susunan rumus luas persegi panjang, maka rumus luas selimut tabung bisa kita tuliskan menjadi:
Luas Selimut Tabung = Panjang Selimut Tabung x Tinggi Tabung
(rumus ini mengikuti susunan rumus persegi panjang)
Oleh karena telah berbentuk melingkar, maka panjang selimut tabung mengikuti rumus keliling lingkaran. Jika keliling lingkaran adalah 2πr dan tinggi tabung adalah t, maka persamaan matematis rumus luas selimut tabung adalah:
Luas Selimut Tabung = 2πr x t
atau
Luas Selimut Tabung = πd x t
atau
Luas Selimut Tabung = πd x t
3. Rumus Luas Selimut Tabung
Setelah melakukan penurunan rumus di atas, maka bisa kita tuliskan dengan mantap bahwa rumus luas selimut tabung adalah:
Luas Selimut Tabung = 2πr x t
atau
Luas Selimut Tabung = πd x t
atau
Luas Selimut Tabung = πd x t
Keterangan:
- r = jari-jari tabung
- d = diameter tabung
- t = tinggi tabung
- π = 22 / 7 atau 3,14
4. Contoh Soal Luas Selimut Tabung
Baiklah, mari kita coba penggunaan rumus di atas untuk menyelesaikan beberapa contoh soal berikut ini:
Contoh Soal 1
Hitunglah luas selimut dari sebuah tabung yang memiliki jari-jari alas 10 cm dan tinggi 12 cm.
 Jawaban:
Jawaban:
Diketahui:

Jawaban:
Diketahui:
Oleh karena kue tart berbentuk tabung, maka sisi sampingnya disebut selimut. Jadi, bagian yang dilapisi coklat adalah selimut tabung. Maka, luas seluruh permukaan kue tart yang dilapisi coklat dihitung menggunakan rumus luas selimut tabung:
Jawaban:
Diketahui:
Jawaban:
Diketahui:

Diketahui:
- r = 10 cm
- t = 12 cm
- Luas Selimut Tabung
- Luas Selimut Tabung = 2πr x t
- = 2 x 3,14 x 10 x 12
- = 753,6
Contoh Soal 2
Sebuah kue tart untuk merayakan ulang tahun berbentuk tabung dengan diameter 28 cm dan tinggi 8 cm. Jika sisi samping kue tart tersebut akan dilapisi coklat, tentukan luas permukaan kue tart yang dilapisi coklat tersebut.
Jawaban:
Diketahui:
- d = 28 cm, r = 28 / 2 = 14 cm
- t = 8 cm
- Luas permukaan kue dilapisi cokelat...?
Oleh karena kue tart berbentuk tabung, maka sisi sampingnya disebut selimut. Jadi, bagian yang dilapisi coklat adalah selimut tabung. Maka, luas seluruh permukaan kue tart yang dilapisi coklat dihitung menggunakan rumus luas selimut tabung:
- Luas Selimut Tabung = 2πr x t
- = 2 x 22 / 7 x 14 x 8
- = 704
Contoh Soal 3
3. Luas selimut tabung yang alasnya berjari-jari 23 cm dan tinggi tabung 7 cm adalah...cm2.Jawaban:
Diketahui:
- r = 23 cm
- t = 7 cm
- Luas selimut tabung...?
- Luas Selimut Tabung = 2πr x t
- = 2 x 22 / 7 x 23 x 7
- = 1.012
Contoh Soal 4
Luas selimut tabung yang memiliki diameter 10 cm dan tinggi 4 cm adalah...Jawaban:
Diketahui:
- d = 10 cm
- t = 4 cm
- Luas selimut tabung...?
- Luas Selimut Tabung = πd x t
- = 3,14 x 10 x 4
- = 125,6
Contoh Soal 5
Luas selimut tabung dengan jari-jari 30 cm dan tinggi 10 cm adalah...Jawaban:
Diketahui:
- r = 30 cm
- t = 10 cm
- Luas selimut tabung...?
- Luas Selimut Tabung = 2πr x t
- = 2 x 3,14 x 30 x 10
- = 2 x 3,14 x 300
- = 3,14 x 600
- = 1.884
Demikianlah penjelasan tentang Rumus Luas Selimut Tabung. Bagikan informasi ini agar orang lain juga bisa membacanya. Terima kasih, semoga bermanfaat.




















0 komentar:
Post a Comment